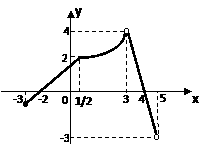Estando eu a procurar por temas interessantes na internet, encontrei este artigo no site da folha.uol (de 25/03/2003) sobre o ensino da Matemática com SUELY DRUCK (presidente da Sociedade Brasileira de Matemática) especial para a Folha de S.Paulo.É interessante notar que trata-se de um artigo feito em 2003, mas cujo conteúdo, infelizmente, ainda é uma realidade no Brasil.
A qualidade do ensino da matemática —assunto da reportagem de capa do último Sinapse— atingiu, talvez, o seu mais baixo nível na história educacional do país.
As avaliações não poderiam ser piores. No Provão, a média em matemática tem sido a mais baixa entre todas as áreas. O último Saeb (Sistema Nacional de Avaliacão da Educacão Básica) mostra que apenas 6% dos alunos têm o nível desejado em matemática. E a comparação internacional é alarmante. No Pisa (Program for International Student Assessment) de 2001, ficamos em último lugar.
Resultados tão desastrosos mostram muito mais do que a má formação de uma geração de professores e estudantes: evidenciam o pouco valor dado ao conhecimento matemático e a ignorância em que se encontra a esmagadora maioria da população no que tange à matemática. Não é por acaso que o Brasil conta com enormes contingentes de pessoas privadas de cidadania por não entenderem fatos simples do seu próprio cotidiano, como juros, gráficos, etc. —os analfabetos numéricos—, conforme atesta o recente relatório Inaf sobre o analfabetismo matemático de nossa população.
Diante dessa situação, encontramos o discurso —tão frequente quanto simplista— de que falta boa didática aos professores de matemática. Todavia, pouco se menciona que o conhecimento do conteúdo a ser transmitido precede qualquer discussão acerca da metodologia de ensino.
Abordar a questão do ensino da matemática somente do ponto de vista pedagógico é um erro grave. É necessário encarar primordialmente as deficiências de conteúdo dos que lecionam matemática. É preciso entender as motivações dos que procuram licenciatura em matemática, a formação que a licenciatura lhes propicia e as condições de trabalho com que se deparam.
A enorme demanda por professores de matemática estimulou a proliferação de licenciaturas. Nas faculdades, há muita vaga e pouca qualidade, o que transforma as licenciaturas em cursos atraentes para os que desejam um diploma qualquer. Produz-se, assim, um grande contingente de docentes mal formados ou desmotivados. Esse grupo atua também no ensino superior, sobretudo nas licenciaturas, criando um perverso círculo vicioso.
É verdade que, nas boas universidades, temos excelentes alunos nas graduações de matemática. Porém, eles formam um grupo tão pequeno que pouco influenciam as tristes estatísticas. Predomina uma enorme evasão dos cursos, uma vez que a maioria não enfrenta as dificuldades naturais dos bons cursos.
Nos últimos 30 anos, implementou-se no Brasil a política da supervalorização de métodos pedagógicos em detrimento do conteúdo matemático na formação dos professores. Comprovamos, agora, os efeitos danosos dessa política sobre boa parte dos nossos professores. Sem entender o conteúdo do que lecionam, procuram facilitar o aprendizado utilizando técnicas pedagógicas e modismos de mérito questionável.
A pedagogia é ferramenta importante para auxi-liar o professor, principalmente aqueles que ensinam para crianças. O professor só pode ajudar o aluno no processo de aprendizagem se puder oferecer pontos de vista distintos sobre um mesmo assunto, suas relações com outros conteúdos já tratados e suas possíveis aplicações. Isso só é possível se o professor tiver um bom domínio do conteúdo a ser ensinado. A preocupação exagerada com as técnicas de ensino na formação dos professores afastou-os da comunidade matemática.
Além disso, eles se deparam com a exigência da moda: a contextualização. Se muitos de nossos professores não possuem o conhecimento matemático necessário para discernir o que existe de matemática interessante em determinadas situações concretas, aqueles que lhes cobram a contextualização possuem menos ainda. Forma-se, então, o pano de fundo propício ao surgimento de inacreditáveis tentativas didático-pedagógicas de construir modelos matemáticos para o que não pode ser assim modelado.
Os Parâmetros Curriculares Nacionais do MEC são erradamente interpretados como se a matemática só pudesse ser tratada no âmbito de situações concretas do dia-a-dia, reduzindo-a a uma sequência desconexa de exemplos o mais das vezes inadequados. Um professor de ensino médio relatou que, em sua escola, existe a "matemática junina", enquanto outro contou ter sido obrigado a dar contexto matemático a trechos de um poema religioso. Certamente, esses não são exemplos de uma contextualização criativa e inteligente que pode, em muito, ajudar nossos alunos. Lamentavelmente, esses tipos de exemplo proliferam em nossas escolas.
O bom treinamento em matemática é efetuado, necessariamente, com ênfase no argumento lógico, oposto ao autoritário, na distinção de casos, na crítica dos resultados obtidos em comparação com os dados iniciais do problema e no constante direcionamento para o pensamento independente. Esses hábitos são indispensáveis em qualquer área do conhecimento e permitem a formação de profissionais criativos e autoconfiantes —e a matemática é um campo ideal para o seu exercício.
O Brasil tem condições de mudar o quadro lastimável em que se encontra o ensino da matemática. Com satisfação, notamos um movimento importante de nossos professores em busca de aperfeiçoamento. Muitos estão conscientes dos problemas de sua formação e dos reflexos que ela tem dentro da sala de aula. Há uma enorme massa de professores que querem ser treinados em conteúdo. O desafio é atingir o maior número de professores no menor espaço de tempo.
Não é verdade que nossas crianças odeiam matemática, conforme prova a participação voluntária de 150 mil jovens e crianças nas Olimpíadas Brasileiras de Matemática de 2002. Muitos mais eles poderiam ser, se os recursos fossem mais abundantes, como é o caso da Argentina, onde 1 milhão participam das Olimpíadas Argentinas de Matemática.
Iniciativas bem-sucedidas existem e apontam caminhos a seguir. Esse é o caso do fantástico programa de matemática coordenado pelo professor Valdenberg Araújo da Silva no interior de Sergipe, que tem levado crianças oriundas de famílias de baixíssima renda a conquistas importantes, como aprovação no vestibular, participação nas olimpíadas e até mesmo início do mestrado em matemática de jovens entre 15 e 17 anos.
Se medidas urgentes não forem tomadas, a situação tenderá a se agravar: há décadas estamos construindo uma sociedade de indivíduos que, ignorando o que é matemática, se mostram incapazes de cobrar das escolas o seu ensino correto ou mesmo apenas constatar as deficiências mais elementares nesse ensino.
Fonte: http://www1.folha.uol.com.br/folha/sinapse/ult1063u343.shtml


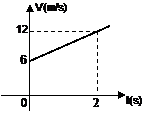

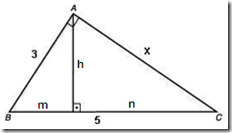
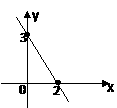
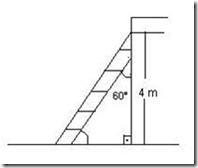
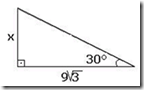 a) 3 b)
a) 3 b) 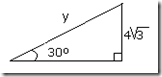
![clip_image002[7] clip_image002[7]](http://lh5.ggpht.com/_fSsSaKPmd2s/S_Rr9O2M62I/AAAAAAAAAgg/TH9iCBqjtOg/clip_image0027_thumb.gif?imgmax=800)
![clip_image002[9] clip_image002[9]](http://lh4.ggpht.com/_fSsSaKPmd2s/S_Rr-tvRtqI/AAAAAAAAAgo/Egeq5g7egBs/clip_image0029_thumb.gif?imgmax=800)